八种方法解一道二元无理式的最小值

题目：已知x>0,y>0,2x+y=2 ,求x+√(x2+y2)的最小值。

解法1：代入消元+判别式法求最小值

由x>0,y>0, 2x+y=2，得y=2-2x，则

解法3  待定系数法助力柯西不等式求最小值

解法4  三角换元+待定系数法+柯西不等式

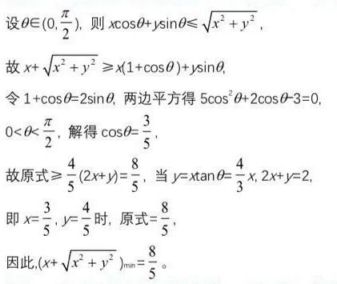
解法5：复合函数求导法求最小值    

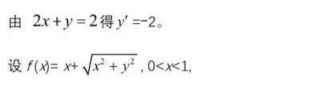
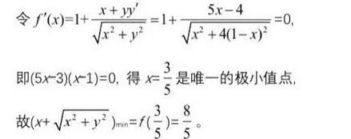
解法6  数形结合法    用角平分线的性质构造对称图形  

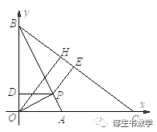
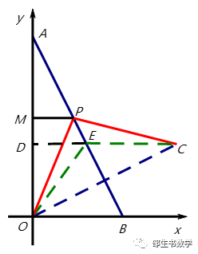
如图，在平面直角坐标系, 设A (1, 0), B (0, 2), 

P (x, y)是线段AB上的动点,设直线OB关于直线AB的对称线为直线BC,

由tan∠OBA=1/2, 

知tan∠OBC=tan2∠OBA=4/3,

得C (8/3, 0), 知直线BC: 3x+4y-8=0,

设P在OB,BC上的垂足分别为D, E,

O在BC上的垂足为H,

则原式=|PD|+|OP|=|OP|+|PE|

≥|OH|=8/√(32+42)=8/5,

当O, P, H三点共线时, 等号成立,

故x+√(x2+y2)的最小值为8/5。 

解法7  用将军饮马问题的方法求最小值  

如图，在平面直角坐标系, 设A (1, 0), B (0, 2), P (x,y)是线段AB上的动点（A,B两点除外）,满足2x+y=2，则x+√(x2+y2)=PM+PO.

作点O关于直线AB的对称点C，可求得点C的坐标为（8/5,4/5）,过点C作y轴的垂线，垂足为D,交AB于点E，则PO=PC,EO=EC.

PM+PO=PM+PC≥CD=8/5,

当点P与点E重合时，等号成立。

故所求式子的最小值为8/5.

解法8   用物理光学性质求解 

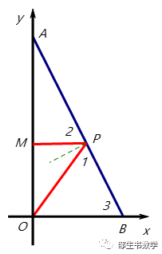
如图，在平面直角坐标系, 设A (1, 0), B (0, 2), P (x,y)是线段AB上的动点（A,B两点除外）,满足2x+y=2，过点P作y轴的垂线，垂足为M,

则x+√(x2+y2)=PM+PO.

根据光在同一媒介里沿最短路径传播这一性质可知，从点O发出的光线射到直线AB发生反射后平行于x轴，这样的光线是存在的，且是唯一的。设平行于 x轴的反射光线与y轴相交于点M，由入射角等于反射角知，

∠1=∠2，又由MP//OB,得∠2=∠3，

所以∠1=∠3，所以OP=OB=1,即x2+y2=1，

又x+2y=2,联立解得x=3/5,

所以PM+PO=3/5+1=8/5.

故所求式子的最小值为8/5.

改编题1：已知x>0,y>0,x+y/3=1 ,

求x+√(x2+y2)的最小值。

改编题2：已知x>0,y>0,x/2+y/3=1 ,

求x+√(x2+y2)的最小值。