换元法求解三大类无理函数的值域
有界性

辅助角公式


配方法

换元法
对于表达式中同时出现sinx±cosx,sinx∙cosx,需要运用(sinx±cosx)2= 1±2sinxcosx的关系式,采用换元的方式转化为二次函数求最值,不过在换元的过程中务必保证旧的变量和新的变量的范围一致。

数形结合法
1直线斜率型
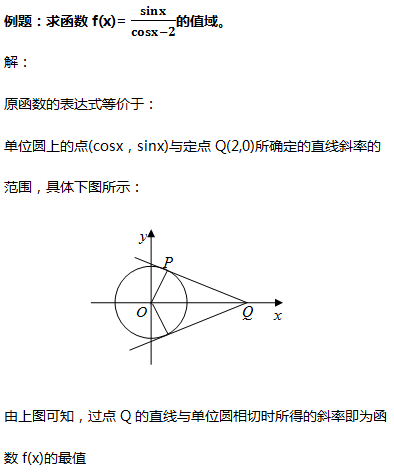

2向量夹角型

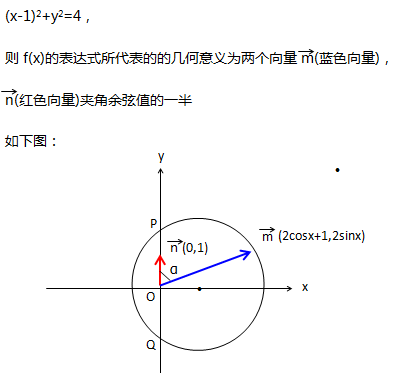

基本不等式法

导数法

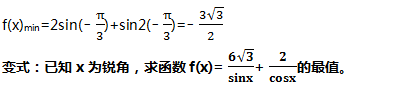
扫描二维码推送至手机访问。
特别声明:
本站属于公益性网站,纯粹个人原因(陪孩子学习便于查询和教授),网站部分内容收集于网络,仅供学生和老师参考、交流使用,请勿用作其他商业收费用途。
如果网站内容能给你带来提升,那便是我经营此网站的初衷。网站相关内容如有问题,请及时提出,我在此谢谢!
本站尊重原创并对原创者的文章表示肯定和感谢,如有侵权请联系删除!针对本站原创内容,本站也欢迎转载,如需转载请注明出处。