结果含参数的极值点偏移问题的解题策略

广东省中山市中山纪念中学(528454) 李文东

极值点偏移问题是近年来高考的热点问题,它常常出现在压轴题的位置,其一般模式如下:

已知函数y = f(x)在区间(a,b)内只有一个极值点x0(非对称轴),函数y = f(x)有两个不同的零点x1,x2,且a ＜x1 ＜x2 ＜b,则有: (1) x1 + x2 ＞2x0(＜2x0); (2)x1·x2 ＞x20(＜x20).

这类问题解决的办法一般是构造对称函数或者是利用对数均值不等式,而最新的一些高三模拟试题中出现了不少结果中含有函数f(x)的参数的极值点偏移问题,这类问题因为所证的结果含有参数,处理起来比较麻烦,本文就这一类结果含有参数的极值点偏移问题的解法作一些探讨.

一般来说,结果含有参数的极值点偏移问题,我们需要先弄清楚函数的零点的范围和极值点的情况,这又需要对函数f(x)分为分离参数和不分离参数这两种情况来考虑.

例1 设函数f(x)=ln x-ax,f(x)有两个不同的零点x1,x2(x1 ＜x2),求a 的取值范围.

解 一方面,由f(x)= ln x - ax = 0 ⇔a = 令g(x)= 则g′(x)=可知g(x)在(0,e)上递增,在(e,+∞)上递减,且g(e)= , g(1)= 0,当x ＞1 时,g(x) ＞0,要使f(x)有两个不同的零点x1,x2,则且1 ＜x1 ＜e ＜x2.

另一方面,由于f(x)有两个零点,显然a ＞ 0,而- a 知f(x)在 递增,在 内递减,得: 0 ＜ a ＜ 且

处理这类问题的关键在于参数,基本原则是消去参数转化为不含参数的问题,具体来说,有以下三个解决策略.

策略1: 利用参数范围放缩

对于结果含有参数的极值点偏移问题,我们可以先求出参数的范围,然后尝试利用这个范围进行适当的放缩,转化为无参数的问题,这一类是结果含参数的极值点偏移问题中较为简单的类型.

例2 设函数f(x)= ln x - ax, f(x)的两个零点为x1,x2(x1 ＜x2).

(1)求证: 

(2)求证:＞2ae.

解 由例1 知: 0 ＜a ＜ 且0 ＜x1 ＜ ＜x2,1 ＜x1 ＜e ＜x2.

(1)要证: ＜ae,只需证: x1 ＜ax2e,由于ax2 ＞1,只需证: ax2e ＞e ＞x1,这显然成立.

(2)又因为0 ＜a ＜所以0 ＜ae ＜1,从而有2 ＞2ae.只需证明:所以

令g(t)=2 ln t-t+ ＜ 0,所以g(t)在(1,+∞)上单调递减,故g(t)＜g(1)=0,命题得证.

例3 (2021年广东省一模)已知函数f(x)=ln x-ax+1

(1)讨论函数f(x)的零点的个数;

(2)设x1,x2 是函数f(x)的两个零点,证明: x1 +x2 +2e ln a ＞0.

分析 结论x1+x2+2e ln a ＞0 中因含有ln a,直接处理比较麻烦,而为f(x)的极值点,联想到一般的极值点偏移问题易得x1+x2 ＞从而将问题转化为 ≥-2e ln a.

解 (1)略.(2)易知: 0 ＜a ＜1,由题意: ln x1 =ax1-1,ln x2 = ax2 - 1,于是ln x2 - ln x1 = a(x2 - x1),所 以由对数均值不等式有: 即x1+x2 ＞只需证: ≥-2e ln a,即a ln a ≥令g(a)=a ln a(0 ＜a ＜1),则g′(a)=1+ln a=0 ⇒a=易知所证成立.

策略2: 利用零点进行参数代换

1.参数代换后变为一元不等式问题,然后构造函数

例4 (2021年温州市高三一模)已知函数f(x)=ln x-ax 有两个不同的零点为x1,x2(x1 ＜x2).

(1)求实数a 的取值范围;

(2)求证: x1 ＜

证明 (1)略.(2)易知: 1 ＜x1 ＜e.要证: x1 ＜只需证: 只需证: e+ax21 ＞2x1.由于a = 故只需证: e+ 即e+x1 ln x1 ＞2x1.令h(t)= e+t ln t-2t,t ∈(1,e),则h′(t)=ln t-1 ＜0 ⇒h(t)＞h(e)=0,所证成立.

例5 (2021年汕头一模)已知函数f(x)= x-ln x-a有两个相异零点为x1,x2(x1 ＜x2).

(1)求a 的取值范围;

(2)求证: x1+x2 ＜

解 (1)略.(2)易知0 ＜ x1 ＜ 1 ＜ x2.要证:x1 + x2 ＜  只需证: x2 ＜ - x1 =-x1 = ,构造函数g(x)=(0 ＜ x ＜ 1),则g′(x)= ＜ 0,所以g(x)在(0,1)上递减, g(x) ＞g(1)= 1.故有x2 ＞＞1.因为f(x)在(1,+∞)上递增,只需证: f(x2) ＜  又f(x2)= f(x1),即证: f(x1) ＜  构造函数h(x)=f(x)-(0 ＜x ＜1),则h′(x)= 下证h′(x)＞0 在(0,1)上恒成立.

变形后即证ln x - ＜ 0,构造函数φ(x)= ln x - ,x ∈ (0,1),则φ′(x)=＞0,故φ(x)在(0,1)上递增,于是φ(x) ＜φ(1)= 0,从 而h′(x) ＞ 0 在(0,1)上恒成立, h(x)在(0,1)上递增,故h(x) ＜ h(1)= 0,即f(x1) ＜

点评 根据零点的含义有x1-ln x1 =a=x2-ln x2,可实现参数a 的代换.

2.参数代换后变为二元不等式问题,然后构造函数

例6 设函数f(x)= ln x -ax, f(x)的两个零点为x1,x2(x1 ＜x2),求证:

(1)

(2)x1+x2 ＞

证明 (1)由题意: ln x1 = ax1,ln x2 = ax2,于是ln x1 + ln x2 = a(x1 + x2),ln x2 - ln x1 = a(x2 - x1),所以= a.要证:  ＞ 2a,只需证:只需证: 令= t ＞ 1,只需证: 2 ln t ＜ t - 令g(t)=则g′(t)= ＜0,所以g(t)在(1,+∞)上单调递减,故g(t) ＜g(1)= 0,命题得证.

(2)要证: x1 + x2＞ - e,只需证:a(x1+x2)(x2-x1) ＞ (3-ae)(x2-x1),只需证:ax22 - ax21 ＞ 3(x2-x1) - e(ax2-ax1),只需证:x2 ln x2 - x1 ln x1 ＞ 3(x2-x1) - e(ln x2-ln x1),只需证: x2 ln x2-3x2+e ln x2 ＞x1 ln x1-3x1+e ln x1.

令g(x)= x ln x - 3x + e ln x(x ＞1),则g′(x)=ln x+ -2, g′′(x)= 故g′(x)在(1,e)上递减,在(e,+∞)上递增,于是g′(x)≥g′(e)=0,g(x)在(1,+∞)上递增,故g(x2)＞g(x1),所证成立.

点评 (1)借助a = (合分比性质),可实现参数a 的代换,尤其是在对数均值不等式中应用广泛;(2)x1+x2 ＞-e 中由于右边含有e 若直接对a 进行代换则很难处理,而本例的处理则很巧妙.

策略3: 对极值点处运用对数均值不等式

例7 设函数f(x)= ln x - ax, f(x)的两个零点为x1,x2(x1 ＜x2),求证: x1+x2 ＞

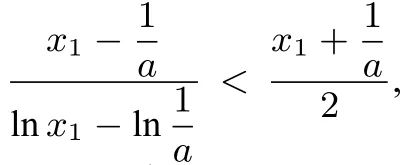证明 显然为f(x)的极值点且x1 ＜ ＜x2,对x1和运用对数均值不等式:由于 化简得(ln x1+ln a),由于ln x1 =ax1,整理得: ax21+(ln a-1)x1+＜0,同理有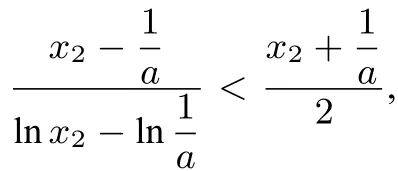整理得: ax22 +(ln a-1)x2 + ＞0,于是ax22 + (ln a-1)x2 +0 ＞ax21+(ln a-1)x1+化简得: (ln a-1)(x2-x1) ＞0,因为x2 ＞x1,于是a(x2+x1) ＞1-ln a,即x1+x2 ＞

本例也可以采用参数代换的方式求解,不过比较复杂,以下解法供读者参考.

证法2 由于a= 要证:x1+x2 ＞

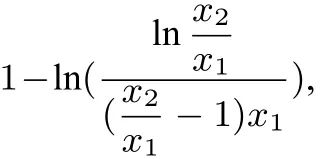只需证: ax1 +ax2 ＞1-ln a,只需证: ln x1 +ln x2 ＞1-只需证: ln x1+ln x2 ＞只需证: ln x2 ＞1-

令=t ＞1,则

只需证: ＞1-ln(ln t)+ln(t-1),令g(t)=1+ln(ln t)-ln(t-1)(t ＞1),则

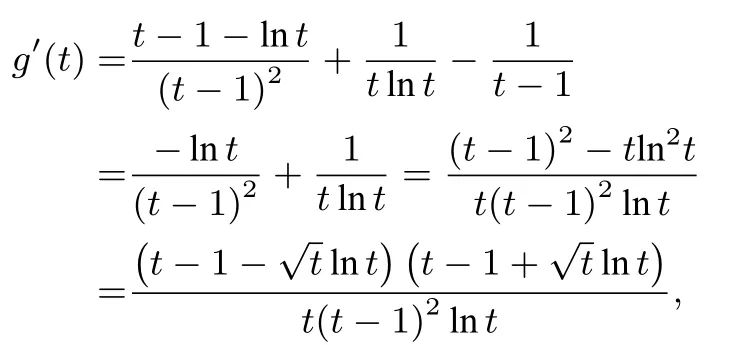
令h(t)=-ln t(t ＞1),则h′(t)=＞0,于是h(t)＞h(1)=0,即＞0,从而g′(t)＞0,于是g(t)在(1,+∞)上递增,又由罗必塔法则 = 1,从而=0,于是g(t)＞0.

例8 已知函数f(x)=(2x-4a)ln x-3x+8a,若f(x)有两个不同的零点x1,x2(x1 ＜x2).

(1)求a 的取值范围;

(2)证明: 当0 ＜x1 ＜e ＜x2 时,x1+x2 ＜

解 (1)a ∈

(2)由f(x)= (2x-4a)ln x-3x+8a = 0,得4a ==g(x),则g′(x)= 显然e 为g(x)的极值点,由于0 ＜x1 ＜e ＜x2,对x1 和e 运用对数均值不等式:即2(x1-e) ＞(x1+e)(ln x1-1),由于f(x1)= (2x1 -4a)ln x1 -3x1 +8a = 0,故ln x1 =代入上面表达式并注意到x1 ＞2a,整理得: 3x21 -(4a+5e)x1 +12ae ＞0,同理有整理得: 3x22-(4a+5e)x2+12ae ＜0,于是3x22-(4a+5e)x2+12ae ＜0 ＜3x21-(4a+5e)x1+12ae,化简得: 3(x22-x21)＜ (4a+5e)(x2-x1),因为x2 ＞x1,于是3(x2+x1)＜4a+5e,即x1+x2 ＜

点评 极值点偏移问题的常见解法一般都是直接对两个零点运用对数均值不等式,由于极值点位于两个零点之间,因此对极值点和两个零点分别运用对数均值不等式效果会更好.