高中数学：拐点的切线

一、拐点的概念

对于可导的函数 f(x)，如果存在某个区间，使得在该点x左侧的区间内f''(x)的符号一致（都为正或都为负），而在x右侧的区间内f''(x)符号相反，那么x点被称为拐点。

从几何角度来看，拐点是曲线凹凸性的转折点。

二、如何计算拐点

最直接的方法是：计算函数的二阶导数f''(x₀)。

如果f''(x₀)=0，f''(x)在该左右符号相反，则(x₀,f(x₀))是拐点。

或者利用三阶导判断：f''(x₀)=0 ,f''(x₀)≠0 则(x₀,f(x₀))为拐点。

拐点具体知识可以查看后面链接：https://yc8.com.cn/wenzhang/202404/4154.html

三、拐点处的切线

在拐点处，切线穿过曲线，且在该点的一侧是曲线的上方，在另一侧是曲线的下方。

比如三次函数 f(x)=x³，原点(0,0)是他的拐点。此处的切线方程为 y=0，这条切线穿过了函数图像。

另外一个例子是大家熟悉的正弦函数 y=sinx，拐点x=0。此处的切线方程为y=x，这条切线在原点会穿过函数，将图像分割成凹性和凸性不同的两部分。

四、具体例题

(2023 杭州二模 ) 已知函数  在点  处的切线方程为: , 若对任意 , 都有  成立, 则 .

「解析」 本题命题背景就是利用拐点处的切线会穿越函数的特点

因为  符号变化时,  符号也会同步发生变化

所以符号不发生改变

看一下图就明白了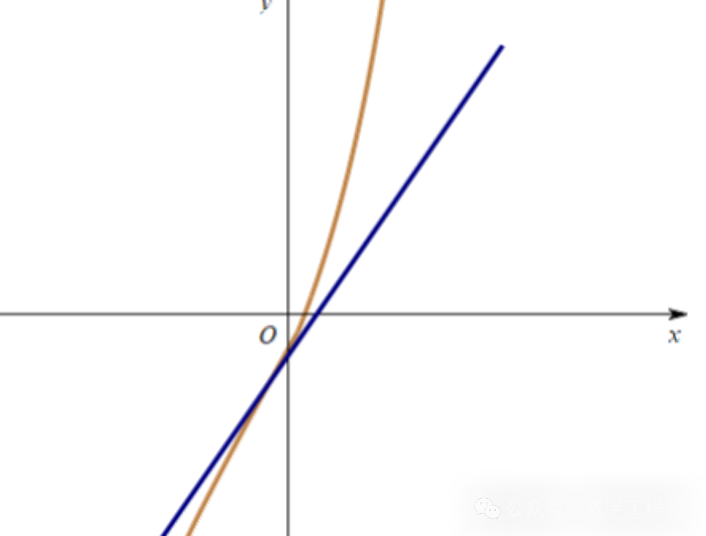

所以题目其实就是在问这个函数的拐点坐标

，

让 , 得 

, 所以 是函数的拐点

(2024河北石家庄高三一模,19) 已知函数 .
(1) 若函数  有 3 个不同的零点, 求  的取值范围;
(2) 已知  为函数  的导函数,  在  上有极小值 0 , 对于某点  在  点的切线方程为 , 若对于 , 都有 , 则称  为好点.
①求  的值; ②求所有的好点.

(1)略 (2) ① ,

令 ,

令 , 可得 ,

 时,  单调递减,

 时,  单调递增,

故 , 解得 .

②显然题目中描述的性质就是拐点处的切线，

, 解得：.

验证一下,所以是拐点，为题目要求的好点。

(2021杭州含周边重点中学联考) (多选) 已知 ( )
A. 若 , 则 , 使函数  有  个零点
B. 若 , 则 , 使函数  有  个零点
C. 若, 则 , 使函数  有  个零点
D. 若, 则 , 使函数  有  个零点

「解析」 本题最莫名其妙的就是  这个数是个什么鬼？

零点问题, 可以数形结合分析

转化为 , 令 

拐点为 , 拐点处的切线为; 

即  这个就是拐点处的切线与  轴的交点

接下来画个草图，当  时，做斜率为负的直线（虚线），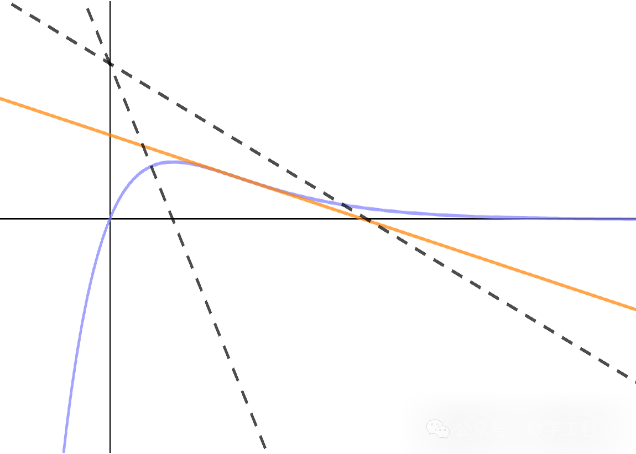

拐点处的切线（橙色）会把图分界, 虚线只会与拐点一侧的曲线相交，无法交出两个点, 所以  错.

对于 ,直线斜率为正时, 做  轴的左边可以实现交两个点

对于 , 当 , 无论斜率大于正还是负, 都显然可以实现.

( 2018 浙江) 已知函数 . (II) 若 , 证明: 对于任意 , 直线  与曲线  有唯一公共点.

「解析」 浙江这道压轴题中, 这个  同样让人莫名其妙

题目与直线和曲线交点个数有关，分析一下拐点的切线

令 , 得 

拐点处的切线为: 

所以  就是拐点切线(绿色）与  轴的交点

当 ,做一条斜率为正的直线（虚线） 和曲线肯定只能有一个交点