排列和组合

一、序言

排列组合是组合学最基本的概念。

所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。

排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。 排列组合与古典概率论关系密切。

二、排列的定义

从n个不同元素中，任取m（m≤n,m与n均为自然数,下同）个不同的元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列；

从n个不同元素中取出m（m≤n）个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号 A(n,m)表示。

排列公式

所谓排列，指的是从互不相同的若干个（n）物品中取出一部分（r），按照顺序排成一列。当这里的r等于n时，我们称之为全排列，即：n×(n-1)×…×3×2×1。有时候，为了表达方便，我们会用n!（n的阶乘）来表示n×(n-1)×…×3×2×1。

三、组合的定义

从n个不同元素中，任取m（m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；

从n个不同元素中取出m（m≤n）个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 或者表示。

组合公式

四、经典应用

1.枚举法：

例题：设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的盒子，现将这5个球投入5个盒子要求每个盒子放一个球，并且恰好有两个球的号码与盒子号码相同，问有多少种不同的方法？

解：2C₅²=20

从5个球中取出2个与2盒子对上号的有C₅²种，还剩下3个球要与3个盒子符号不能对上，利用枚举法，如果剩下的是3，4，5号球，3号球如果装4号盒时，则4，5号球只有1种装法，同理3号球装5号盒时，4，5号球也只有1种装法，所以总共是有2种装法。因此最终的结果为2C₅²。

点评：

元素比较少的，又比较复杂的排列组合问题，可以用枚举法得到意想不到的结果。

变式：将数字1，2，3，4填入标号为1，2，3，4的四个方格里，每格填一个数，则每个方格的标号与所填数字均不相同的填法有多少种？

2.捆绑法：

例题：7人站成一排，其中甲乙相邻且丙丁相邻，共有多少种不同的排法

解：A⁵₅A²₂A²₂=480

点评：

要求某几个元素必须排在一起的问题，可以用捆绑法来解决，将需要相邻的元素合并为一个元素，再与其他元素一起作排列，同时要注意合并元素内部也必须排列。

变式：七个家庭一起外出旅游，若其中四家是男孩，三家是女孩，现将这七个小孩拍成一排照相留念。若三个女孩要站在一起，四个男孩也要站在一起，共有多少种不同的排法？

3.插空法：

例题：7人站成一排，其中甲乙两人不能相邻，共有多少种不同的排法

解：

A⁵₅C²₆A²₂=3600

点评：

元素不相邻问题，可以先把没有位置要求的元素进行排序，然后再根据题意将不相邻的元素插到已经排序完成的元素之中。

变式：马路上有编号为1，2，3……9的九盏路灯，为节约用电，现要求把其中三盏灯，但不能关掉相邻的2盏或3盏，也不能关掉两端的路灯，满足条件的关灯方法有几种？

4.定序缩倍法：

例题：7人站成一排，其中甲乙丙三人顺序一定，共有多少种不同的排法

解：

A⁷₇/A³₃=840

点评：

对于某几个元素顺序一定的排列问题，可先把这几个元素与其他元素一起进行排列，然后用总排列数除以这几个元素之间的全排列数，即是所得结果。

变式1：10人身高各不相同，排成前后排，每排5人，要求从左至右身高逐渐增加，共有多少种排法？

变式2：将3个完全相同的红球与5个完全相同的白球排成一排，共有多少种排法？

5.特殊定位优先法：

例题：1名老师和4名获奖同学排成一排照相留念，若老师不站两端则有不同的排法有多少种？

解：

C¹₃A⁴₄=72

总共有5个位置，因为老师不站在两端，所以从中间的3个位置选1个，剩下的4位学生全排列。

点评：

某个或几个元素要排在指定位置，可先排这个或几个元素；再排其它的元素。

变式：由0，1，2，3，4，5可以组成多少个没有重复的五位奇数？

6.多排问题单排法：

例题：6个不同的元素排成前后两排，每排3个元素，那么不同的排法种数有几种？

解：

A⁶₆=120

点评：

把元素排成几排的问题可归结为一排考虑，再分段研究

变式1：8个不同的元素排成前后两排，每排4个元素，其中某2个元素要排在前排，某1个元素排在后排，有多少种不同排法？

变式2：10名学生分坐两行，要求面对面坐下，但其中甲乙两位同学不可相邻也不可面对面，有多少种做法？

7.同元素分配隔板法：

（1）每份至少含有1个元素

例题：10个三好学生名额分到7个班级，每个班级至少一个名额，有多少种不同分配方案？

解：

C⁶₉=84

点评：

将n个相同的元素分成m份，每份至少一个元素，可以用m-1块隔板，插入n个元素排成一排的n-1个空隙中，所有分法为

变式：7个相同的小球，任意放入4个不同的盒子中，每个盒子至少有一个小球的不同放法有多少种？

（2）其中一分或几分中可以含有0个元素

例题：10个三好学生名额分到7个班级，有多少种不同分配方案？

解：

C⁶₁₆=8008

点评：

将n个相同的元素分成m份，并未提及每份至少含有一个元素，即可以含有0个元素的情况，这时用“元素数(n)+隔板数(m-1)”为总的元素数，分成4份，所有分法为C^m-1_n+m-1。

变式：7个相同的小球，任意放入4个不同的盒子中，不同放法有多少种？

8.不同元素平均分配法：

例1：将6本不同的书，平均分成三份的分法有多少种？

解：

C²₆C²₄C²₂/A³₃=15

点评：

对于平均分堆问题，是与顺序无关的，所以组合数相乘后要除以

A^m_m,其中m表示均分的组数。很多同学不理解为什么要除以组数的阶乘，举个例子，三个不同的苹果，分成三份，总共有几种分法？很显然只有一种，计算式子为C¹₃C¹₂C¹₁/A³₃，而不是C¹₃C¹₂C¹₁，这样就会比较好理解一些。

变式：将10名同学平均分成5个组，总共有多少种分法？

例2：将6本不同的书，分成三份，一份有4本，另外两份各1本的分法有多少种？

解：

C⁴₆.(C¹₂C¹₁/A²₂)=15

点评：

对于非均分的问题，只需要组合数相乘，如果题目中即含有均分问题又含有非均分问题(如上面例2)，组合数相乘之后只需要除以均分组数的阶乘。

变式：8本不同的书分成三份，其中1份2本，另外两份各3本，有多少种不同的分法？

9.先选后排法：

例题：将6本不同的书，平均分给3名同学的分法有多少种？

解：

(C²₆C²₄C²₂/A³₃).A³₃=90

点评：

这类题目属于排列组合的混合问题，遵循的最基本的规则为先选后排，即先分组后排序。

变式1：8本不同的书分给3名同学，其中1名同学2本，另外两人3本，有多少种不同的分法？

变式2：有5个不同的小球，装入4个不同的盒内，每盒至少装一个球，共有多少不同的装法？

变式3：将6本不同的书分给甲乙丙三个人，每人至少一本的分法有多少种？

10.合理分类法：

例题：某高校从某系的10名优秀毕业生中选4人分别到西部四城市参加中国西部经济开发建设，其中甲同学不到银川，乙不到西宁，共有多少种不同派遣方案？

解：

(1)甲乙均未被选中：A⁴₈

(2)甲被选中乙未被选中：C³₈C¹₃A³₃

先从除了甲乙两人以外的8个人中选三人，且甲被选中，现在已经选择了4个人，因为甲不能去银川，所以从另外三个地方选一个，其余三个人全排列。

(3)乙被选中甲未被选中：C³₈C¹₃A³₃

(4)甲乙均被选中：C²₈(A⁴₄-A³₃-A³₃+A²₂)

先从除了甲乙两人以外的8个人中选两人，且甲，乙都被选中，现在已经选择了4个人，4个人全排列A⁴₄之后，要减去甲在银川的A³₃（不管乙的位置)，再减去乙在西宁A³₃的（不管甲的位置)。那为什么最后还要再加上A²₂呢？因为甲在银川的时候，存在乙可能在西宁的情况；同样乙在西宁的时候，存在甲在银川的情况，因此多减了一次甲在银川乙在西宁的情况，因此要再加上A²₂。

点评：

元素多，取出的情况也多种，可按结果要求分成不相容的几类情况分别计数，最后总计。

变式1：从6名运动员中选出4人参加4×100米接力赛，如果甲不跑第一棒，乙不跑第四棒，共有多少种不同的参赛方案？

变式2：在一次演唱会上共有10名演员，其中8人能唱歌，5人能跳舞，现将演出一个2人唱歌2人伴舞的节目，总共有多少种选派的方法。

11.排除法：

例题：以正方体的顶点为顶点的四面体总共有多少种？

解：

C⁴₈-6-6=58

从下图正方体可以看出，同一个面的四个顶点，是不能组成四面体的，要排除，总共有6种可能.

另外从下图正方体还可以看出，对角面上的四个顶点，也是不能组成四面体的，要排除，总共也有6种可能

点评：

在选取的总数中，只有一部分合条件，可以从总数中减去不符合条件数，即为所求.

变式1：四面体的顶点和各棱中点共10个点，从中取4个不共面的点，不同的取法有多少种？

变式2：从4台甲型和5台乙型电视机中任取3台，其中至少要甲型和乙型电视机各一台，则不同的取法共有多少种？

12.一个班级有10位同学，现在要选出班委会，其中：一位班长，一位副班长，一位学习委员，一位组织委员。请问：一共有多少种选举班委会的方法？

因为一个班级的10位同学都是有可能成为班长的，所以选班长有10种可能性；同理，一位同学成为班长后，剩余的9位同学都有可能成为副班长；以此类推。

因此，选举班委会的方法一共有10×9×8×7＝5040种。

13.在一个8×8的方格棋盘上，放入8枚棋子，要求任意两枚棋子都不在同一行同一列上，请问有多少种放法？

我们可以以每一列或者每一行为出发点。对于第一列而言，有8个位置可供第一枚棋子放；对于第二列而言，有7个位置可供第一枚棋子放；……；以此类推。

因此，全部的放法为8×7×6×5×4×3×2×1＝8!＝40320种。

14.小明路过一家丸子店，看到店铺门口登了一则广告：本店供应鸡肉丸、牛肉丸、章鱼丸、鱼丸、羊肉丸和虾肉丸，请问4个不同的丸子串在一起有多少种不同的排列方式？答对者可享受五折优惠购买本店的丸子。

有了前面的经验，这道题应该就很显然了。一共有6×5×4×3＝360种排列方式。如下图所示：

15.有A、B、C、D、E五位同学站成一排拍合照，其中A和B两人一定要排在一起，共有多少种不同的排法？

这里，如果直接去计算的话会很麻烦，我们可以把A和B看成整体，于是5个人的排列问题就转变为了4个人的排列。

又因为A、B是可以互换位置的，所有一共有4!×2＝48种排法。

16.有一个圆桌，共有五个座位。现在有五个人要坐在这些座位上，请问一共有几种入座方式？

这道题看上去很简单，实际上有一定难度。

很多同学第一眼看到这个问题时，都会想当然地回答：5!＝5×4×3×2×1＝120种。真的是这样吗？

要回答这个问题，就要先理解圆桌和长桌的座位有什么区别。假如现在不是圆桌，而是长桌。如下图所示：

假设现在有A、B、C、D、E这五个人入座，ABCDE是一种就座的顺序，EABCD也是一种顺序，DEABC又是一种顺序，……。之所以称为不同的就座顺序，是因为对于这里的每个人而言，他们左右的邻居或多或少都发生了一些变化。因此，就长桌而言，答案就是5!＝5×4×3×2×1＝120种。

那么圆桌呢？与长桌相比，又有什么变化？我们发现，下面这五种情况虽然在长桌上属于不同的情况，但在圆桌上其实是一种情况，因为对于这五人中的任何一位而言，无论怎么入座，他的左右领座都没有发生变化，所以属于同一种顺序。

因此，上述问题的答案就是5!/5＝4!＝24种，这里除以5是把五种相同的重复情况剔除掉。

有了前面的解释和基础，这个问题还可以换个角度来看。我们可以让一个人（比如A）先找其中一个座位坐下来，这样就不存在“转”的问题了。因此，剩下的4个人就有4!种坐法。

17.将五颗不同的宝石串成一圈，做成一串手串，共有多少种不同的串法？

这个问题初看上去与例5没啥区别。但事实上，两者之间存在一些细微的区别。

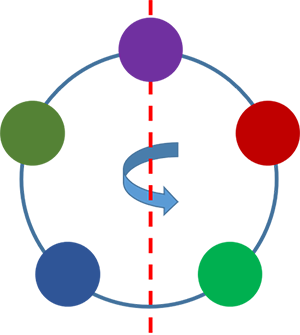
因为，对于任何一种顺序而言，假如翻转一下，在圆桌问题上是两种不同的顺序，而在这个手串的问题上，则是同一串手串。

因此，本题的答案是4!÷2＝12种串法。