圆锥曲线选填压轴小题之面积问题
圆锥曲线选填压轴小题之面积问题
【基本知识】
1、弦长问题:设圆锥曲线
直线
则
直线
4.平行四边形的面积:
直线
(1)在
【基本技能】
1、面积问题的解决策略:
(1)求三角形的面积需要寻底找高,需要两条线段的长度,为了简化运算,通常优先选择能用坐标直接进行表示的底(或高)。
(2)面积的拆分:不规则的多边形的面积通常考虑拆分为多个三角形的面积和,对于三角形如果底和高不便于计算,则也可以考虑拆分成若干个易于计算的三角形.
(3)多个图形面积的关系的转化:关键词“求同存异”,寻找这些图形的底和高中是否存在“同底”或“等高”的特点,从而可将面积的关系转化为线段的关系,使得计算得以简化.
2、面积范围的解决策略:
通常利用公式将面积转化为某个变量的函数,再求解函数的最值,在寻底找高的过程中,优先选择长度为定值的线段参与运算。这样可以使函数解析式较为简单,便于分析.
方法:首选均值不等式或对勾函数,其实用二次函数配方法,最后选导数思想.
均值不等式 :
作用:当两个正数的积为定值时求出这两个正数的和的最小值;
当两个正数的和为定值时求出这两个正数的积的最大值!
注意:应用均值不等式求解最值时,应注意“一”正“二”定“三”相等
圆锥曲线经常用到的均值不等式形式:
1)
2)
3)
4)
5)
6)


【答案】
【解析】


【答案】B
【解析】


【答案】B
【解析】
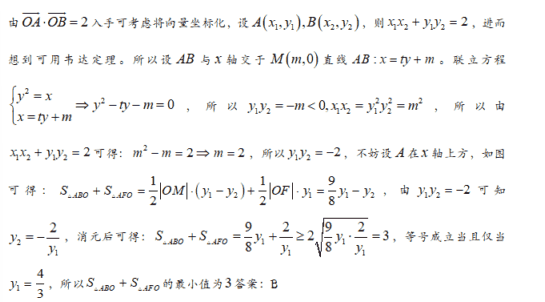

【答案】A
【解析】


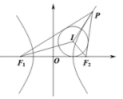
【答案】C
【解析】

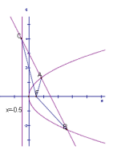
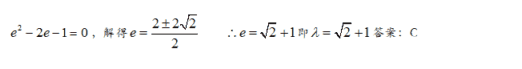
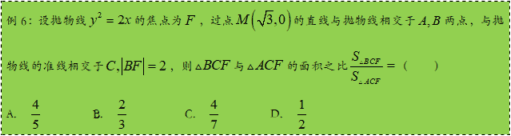
【答案】A
思路:

【解析】
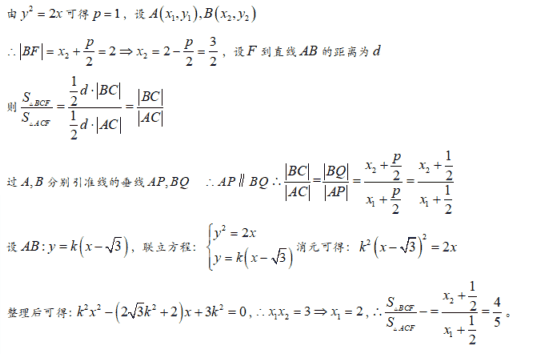

【证明】
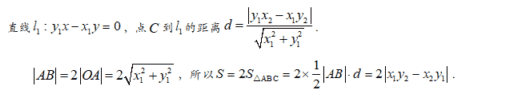
【提高训练】(共27题)
部分详细解析文末获取!!
部分详细解析文末获取!!
部分详细解析文末获取!!
一、单选题

【答案】C
【解析】
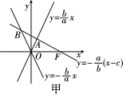
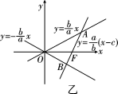
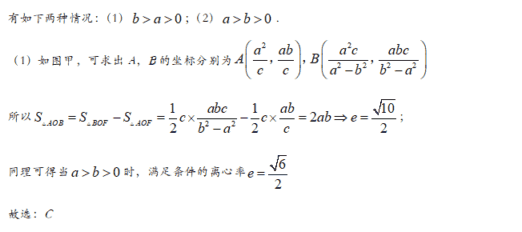

【答案】B
【解析】
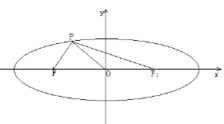


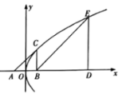
【答案】B
【解析】
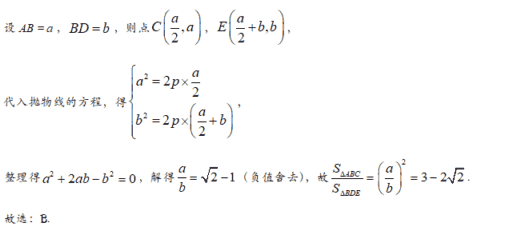

【答案】D
【解析】
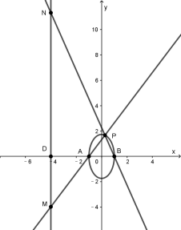


【答案】B
【解析】
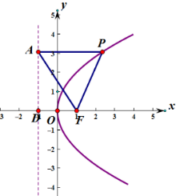


【答案】C

【答案】C

【答案】C

【答案】A

【答案】D
学科网][来源:学#科#网Z#X#X#K][来源:学科网]

【答案】C

【答案】C

【答案】D

【答案】A

【答案】C

【答案】A

【答案】B
【解析】
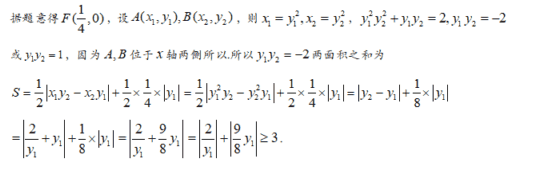

【答案】C
【解析】


【答案】A
【解析】

一、填空题

【答案】3.
【解析】
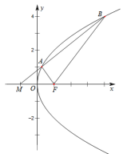
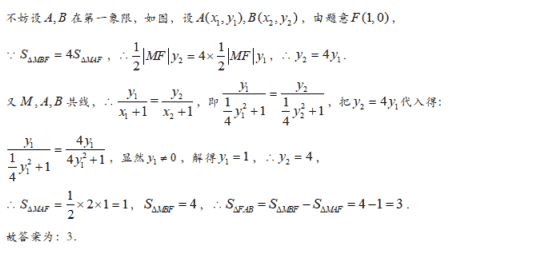

【答案】8
【解析】
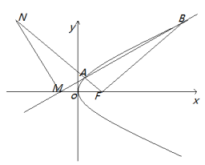



【答案】4
【解析】
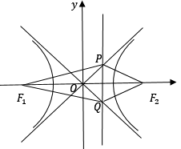
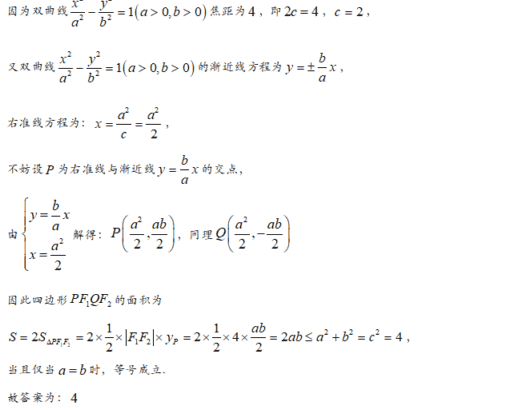

【答案】

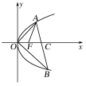
【答案】3

【答案】

【答案】

【答案】
【解析】
扫描二维码推送至手机访问。
特别声明:
本站属于公益性网站,纯粹个人原因(陪孩子学习便于查询和教授),网站部分内容收集于网络,仅供学生和老师参考、交流使用,请勿用作其他商业收费用途。
如果网站内容能给你带来提升,那便是我经营此网站的初衷。网站相关内容如有问题,请及时提出,我在此谢谢!
本站尊重原创并对原创者的文章表示肯定和感谢,如有侵权请联系删除!针对本站原创内容,本站也欢迎转载,如需转载请注明出处。