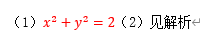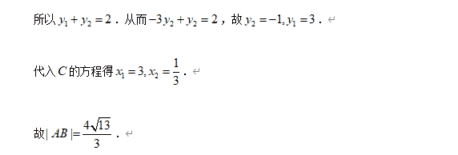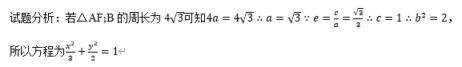圆锥曲线11大常考题型 近5年真题汇总
圆锥曲线11大常考题型 近5年真题汇总
题型十一：存在性问题（存在点、直线y=kx+b、实数、圆形、三角形、四边形等）题型十一：存在性问题（存在点、直线y=kx+b、实数、圆形、三角形、四边形等）(1)直接法：根据圆的几何性质，直接求出圆心坐标和半径，进而写出方程。①若已知条件与圆心和半径有关，则设圆的标准方程依据已知条件列出关于的方程组，从而求出的值；②若已知条件没有明确给出圆心或半径，则选择圆的一般方程，依据已知条件列出关于D、E、F的方程组，进而求出D、E、F的值。刷有所得：该题考查的是有关直线与椭圆的问题，涉及到的知识点有直线方程的两点式、直线与椭圆相交的综合问题、关于角的大小用斜率来衡量，在解题的过程中，第一问求直线方程的时候，需要注意方法比较简单，需要注意的就是应该是两个，关于第二问，在做题的时候需要先将特殊情况说明，一般情况下，涉及到直线与曲线相交都需要联立方程组，之后韦达定理写出两根和与两根积，借助于斜率的关系来得到角是相等的结论.
例12：刷有所得：椭圆定义的应用主要有两个方面：一是判断平面内动点与两定点的轨迹是否为椭圆，二是利用定义求焦点三角形的周长、面积、椭圆的弦长及最值和离心率问题等；“焦点三角形”是椭圆问题中的常考知识点，在解决这类问题时经常会用到正弦定理，余弦定理以及椭圆的定义.刷有所得：求离心率的值或范围就是找的值或关系。由想到点M的轨迹为以原点为圆心，半径为的圆。再由点M在椭圆的内部，可得，因为 。所以由得，由关系求离心率的范围。刷有所得：本题主要考查椭圆的定义及离心率以及双曲线的定义及离心率，属于中档题. 离心率的求解在圆锥曲线的考查中是一个重点也是难点，一般求离心率有以下几种情况：①直接求出，从而求出;②构造的齐次式，求出;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解．刷有所得：解决椭圆和双曲线的离心率的求值及取值范围问题，其关键就是确立一个关于的方程或不等式，再根据的关系消掉得到的关系式，而建立关于的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
扫描二维码推送至手机访问。
特别声明：
本站属于公益性网站，纯粹个人原因（陪孩子学习便于查询和教授），网站部分内容收集于网络，仅供学生和老师参考、交流使用，请勿用作其他商业收费用途。
如果网站内容能给你带来提升，那便是我经营此网站的初衷。网站相关内容如有问题，请及时提出，我在此谢谢！
本站尊重原创并对原创者的文章表示肯定和感谢，如有侵权请联系删除！针对本站原创内容，本站也欢迎转载，如需转载请注明出处。
本文链接：https://yc8.com.cn/wenzhang/202112/835.html
“圆锥曲线11大常考题型 近5年真题汇总” 的相关文章
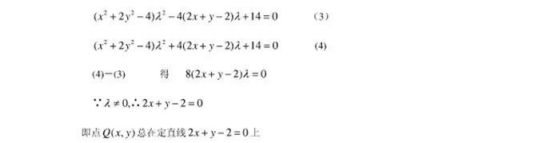
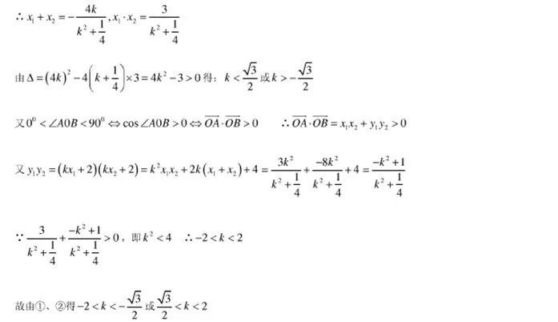
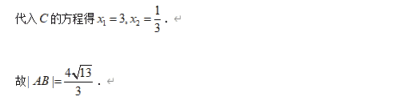
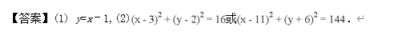
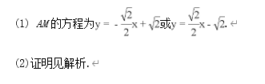
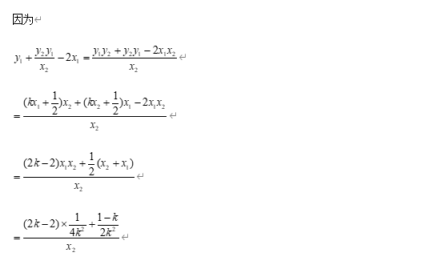
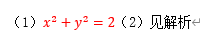
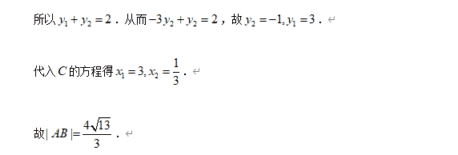
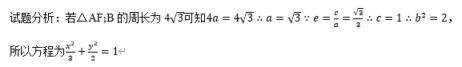
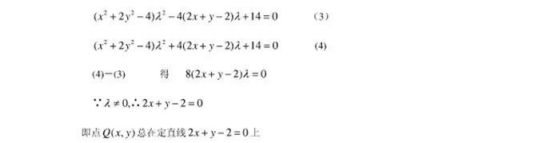
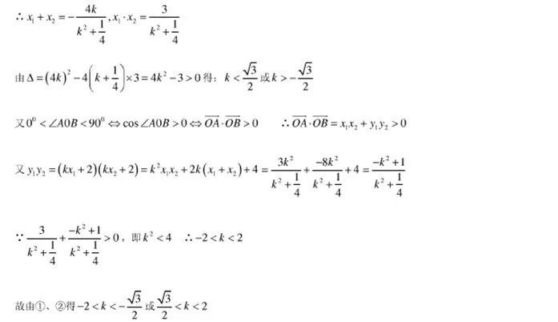
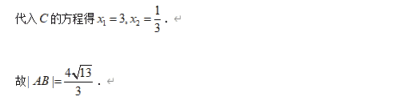
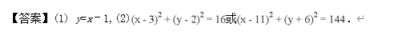
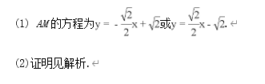
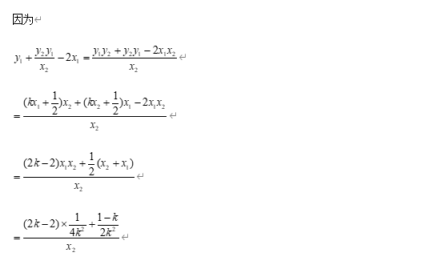
例12：
