综述

一、考情分析

通过对近几年的高考试题的分析比较发现,高考对直线与圆的考查,呈现逐年加重的趋势,与圆有关的最值问题,更是高考的热点问题.由于圆既能与平面几何相联系,又能与圆锥曲线相结合,命题方式比较灵活,故与圆相关的最值问题备受命题者的青睐.

二、经验分享

1. 与圆有关的最值问题的常见类型及解题策略

(1)与圆有关的长度或距离的最值问题的解法．一般根据长度或距离的几何意义，利用圆的几何性质数形结合求解．

三、知识拓展

四、题型分析

(一) 与圆相关的最值问题的联系点

1.1 与直线的倾斜角或斜率的最值问题

【答案】C

【解析】

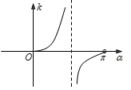
【点评】由斜率取值范围确定直线倾斜角的范围要利用正切函数y＝tan x的图象,特别要注意倾斜角取值范围的限制；求解直线的倾斜角与斜率问题要善于利用数形结合的思想,要注意直线的倾斜角由锐角变到直角及由直角变到钝角时,需依据正切函数y＝tan x的单调性求k的范围．

【答案】B

【解析】

1.2 与距离有关的最值问题

在运动变化中,动点到直线、圆的距离会发生变化,在变化过程中,就会出现一些最值问题,如距离最小,最大等.这些问题常常联系到平面几何知识,利用数形结合思想可直接得到相关结论,解题时便可利用这些结论直接确定最值问题.

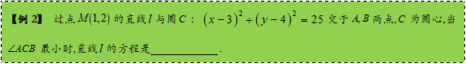
【答案】  

【解析】

【点评】与圆有关的长度或距离的最值问题的解法．一般根据长度或距离的几何意义,利用圆的几何性质数形结合求解．此题通过两次转化,最终转化为求过定点的弦长最短的问题.

【答案】C

【解析】

【点评】与切线长有关的问题及与切线有关的夹角问题,解题时应注意圆心与切点连线与切线垂直,从而得出一个直角三角形．

1.3  与面积相关的最值问题

 与圆的面积的最值问题,一般转化为寻求圆的半径相关的函数关系或者几何图形的关系,借助函数求最值的方法,如配方法,基本不等式法等求解,有时可以通过转化思想,利用数形结合思想求解.

【答案】A

【解析】

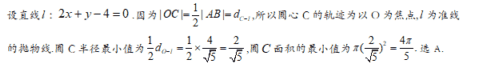
【答案】D

【解析】

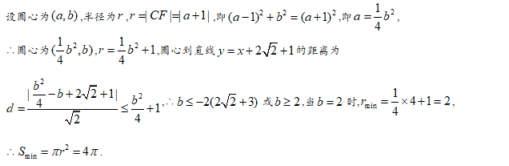
【答案】C

【解析】

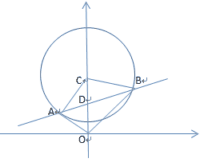
(二) 与圆相关的最值问题的常用的处理方法

2.1 数形结合法

处理与圆有关的最值问题,应充分考虑圆的几何性质,并根据代数式的几何意义,借助数形结合思想求解.

【分析】(1)利用斜率模型；(2)利用截距模型；(3)利用距离模型

【解析】

【点评】研究与圆有关的最值问题时,可借助图形的性质,利用数形结合求解．常见的最值问题有以下几种类型：①形如  型的最值问题，可转化为过点(a，b)和点(x，y)的直线的斜率的最值问题；②形如t＝ax＋by型的最值问题，可转化为动直线的截距的最值问题；③形如  型的最值问题，可转化为动点到定点(a，b)的距离平方的最值问题．

【答案】B

【解析】

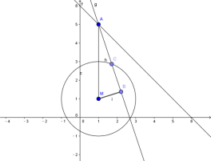
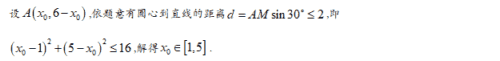
2.2 建立函数关系求最值

根据题目条件列出关于所求目标函数的关系式,然后根据关系的特点选用参数法、配方法、判别式法等进行求解.

【答案】D

【解析】

2.3 利用基本不等式求解最值

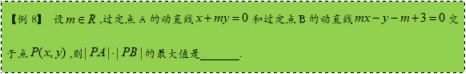
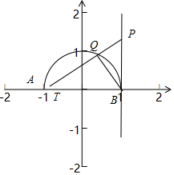
【答案】5

【分析】根据  ,可用均值不等式求最值

【解析】

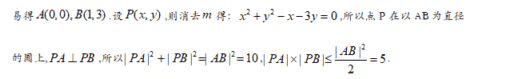
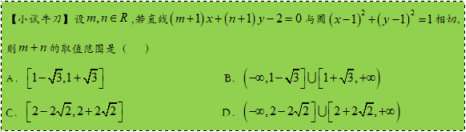
【答案】D

【解析】

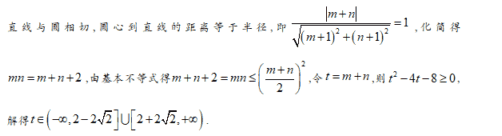
四、提高训练（共23道题）

详细解析文末获取！！！

详细解析文末获取！！！

详细解析文末获取！！！

【答案】A

【解析】

【答案】C

【答案】B

【解析】

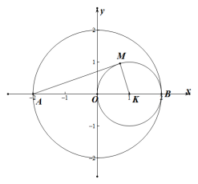
【答案】D

【答案】C

【答案】C

【答案】A

【答案】D

【解析】

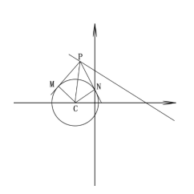
【答案】D

【解析】

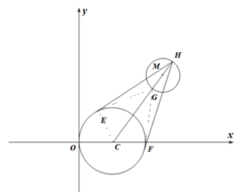
【答案】A

【解析】

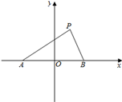
【答案】B

【答案】C

【答案】D

【解析】

【答案】C

【答案】B

【答案】C

【答案】A

【答案】B

【答案】C

【答案】  

【答案】  

【答案】