探究递推公式为分式型数列的通项问题

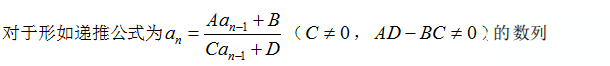
这类问题有一般性的公式解法，通常用特征方程求不动点，即先求解递推公式所对应的特征方程，求出不动点，然后再解。

虽然这类题本身有特征方程求不动点等的知识背景，但高考题并不考，也不依赖于这知识，从所给的标准答案来看，其立意在于将递推数列求通项问题转化为已知数列的已知知识来解决，即转化为等差数列或等比数列来解决。

那么，有没有不用高等数学知识，而只用高中数学知识的方法？这类问题是否存在通项公式？若存在又怎么来求？下面通过具体例子介绍一种方法，仅供参考!

以上方法尽管相对较麻烦些，但它用得知识点和方法都是高中数学内容所要求的。因为原数列既不是等差数列也不是等比数列，但我们在原数列上“加”上一个适当的数，再“倒”过来，就可以用我们所掌握的等差，等比知识来求了，所以不妨称之为“加倒法”。它是一种初等的方法。