高中数学:异面直线的距离的六种求法
高中数学:异面直线的距离的六种求法
已知正方体ABCD-A1B1C1D1的棱长为1,求异面直线A1D与AC的距离。
1.方法一
一、直接利用定义求解
如图1,取AD中点M,连MD1、MB分别交A1D、AC于E、F,连BD1,由平面几何知识,易证ME=1/3MD1,MF=1/3MB,MD1=MB,则BD1//EF。
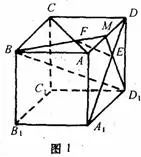
由![]() ,
,![]() 得
得![]() ⊥平面
⊥平面![]() ,则
,则![]() ,同理AC⊥
,同理AC⊥![]() ,所以,EF⊥
,所以,EF⊥![]() ,EF⊥AC,即EF为异面直线
,EF⊥AC,即EF为异面直线![]() 与AC的距离,故有EF=
与AC的距离,故有EF=![]() 。
。
此法的关键是作出异面直线的公垂线段。
2.方法二
二、转化为线面距离求解
如图2,连![]() 、
、![]() ,则AC∥平面
,则AC∥平面![]() 。设AC、BD交于O,
。设AC、BD交于O,![]() 、
、![]() 交于
交于![]() ,连
,连![]() ,作OE⊥
,作OE⊥![]() 于E,由
于E,由![]() ⊥平面
⊥平面![]() 知
知![]() ,故OE⊥平面
,故OE⊥平面![]() 。
。
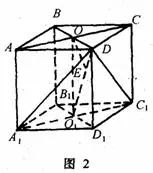
所以OE为异面直线![]() 与AC的距离。
与AC的距离。
在![]() △
△![]() 中,
中,![]() ,则
,则
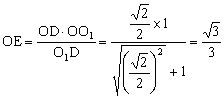 。
。
所以异面直线![]() 与AC的距离为
与AC的距离为![]() 。
。
此法是将线线距离问题转化为线面距离问题来解,合理、恰当地转化是解决问题的关键。
3方法三
三、转化为面面距离求解
如图3,连![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,易知平面
,易知平面![]() ,则异面直线
,则异面直线![]() 与AC的距离就是平面
与AC的距离就是平面![]() 与平面
与平面![]() 的距离,易证
的距离,易证![]() ⊥
⊥![]() 、
、![]() ⊥平面
⊥平面![]() ,且
,且![]() 被平面
被平面![]() 和平面
和平面![]()
三等分,又![]() 。
。
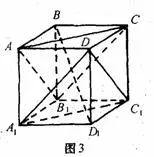
所以异面直线![]() 与AC的距离为
与AC的距离为![]() 。
。
此法是将线线距离问题转化为面面距离问题来解,巧妙的转化常能收到事半功倍的奇特效果。
4. 方法四
四、构造函数求解
如图4,在![]() 上任取一点E,作EM⊥AD于M,再作MF⊥AC于F,连EF,则∠EMF=
上任取一点E,作EM⊥AD于M,再作MF⊥AC于F,连EF,则∠EMF=![]() 。
。
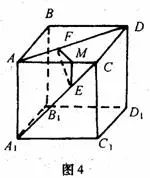
设MD=![]() ,则ME=
,则ME=![]() ,AM
,AM![]() ,在
,在![]() 中,∠FAM=
中,∠FAM=![]() ,则
,则![]()
所以
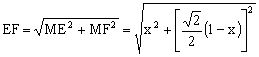
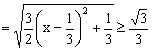 ,
,
当且仅当![]() 时,EF取最小值
时,EF取最小值![]() 。
。
所以异面直线![]() 与AC的距离为
与AC的距离为![]() 。
。
选取恰当的自变量构造函数,即可利用函数的最小值求得异面直线间的距离。
5. 方法五
五、利用体积变换求解
如图5,连![]() 、
、![]() 、
、![]() ,则
,则![]() ∥平面
∥平面![]() ,设异面直线
,设异面直线![]() 与AC的距离为
与AC的距离为![]() ,则D到平面
,则D到平面![]() 的距离也为
的距离也为![]() 。
。
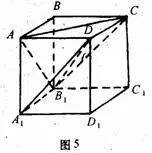
易知
![]() ,
,
![]() 。
。
由![]() ,
,
得![]() 。
。
所以![]() ,则
,则![]() 。
。
所以异面直线![]() 与AC的距离为
与AC的距离为![]() 。
。
此法是将异面直线的距离转化为锥体的高,然后利用体积公式求之。
6
方法六
六、利用向量求解
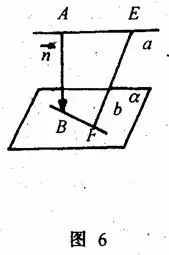
如图6,AB为异面直线![]() 、
、![]() 的公垂线段,
的公垂线段,![]() 为直线AB的方向向量,E、F分别为直线
为直线AB的方向向量,E、F分别为直线![]() 、
、![]() 上的任意一点,则
上的任意一点,则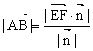 。
。
证明:显然![]() =
=![]() ,
,![]() ,
,![]() 。
。
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
即![]() ,
,
所以![]() 。
。
把上述结论作为公式来用,即可巧妙地求出某些问题中的异面直线间的距离。
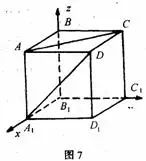
建立如图7所示的空间直角坐标系,易知
![]() ,
,
![]() =(-1,1,0),
=(-1,1,0),
![]() (-1,0,0)。
(-1,0,0)。
设异面直线
![]() 、AC的公垂线的方向向量为
、AC的公垂线的方向向量为
![]() ,由
,由![]() ,
,![]() ,得
,得
![]()
解得
![]()
故可取
![]() 。
。
所以异面直线
![]() 与AC的距离为
与AC的距离为![]() 。
。
此法是利用公式求解,具有不必作出公垂线段的特点,合理、恰当地建立空间直角坐标系,常能使问题变得简单易解。
扫描二维码推送至手机访问。
特别声明:
本站属于公益性网站,纯粹个人原因(陪孩子学习便于查询和教授),网站部分内容收集于网络,仅供学生和老师参考、交流使用,请勿用作其他商业收费用途。
如果网站内容能给你带来提升,那便是我经营此网站的初衷。网站相关内容如有问题,请及时提出,我在此谢谢!
本站尊重原创并对原创者的文章表示肯定和感谢,如有侵权请联系删除!针对本站原创内容,本站也欢迎转载,如需转载请注明出处。