初中几何：圆相关几何知识点

知识点及公式整理

圆中辅助线添加技巧

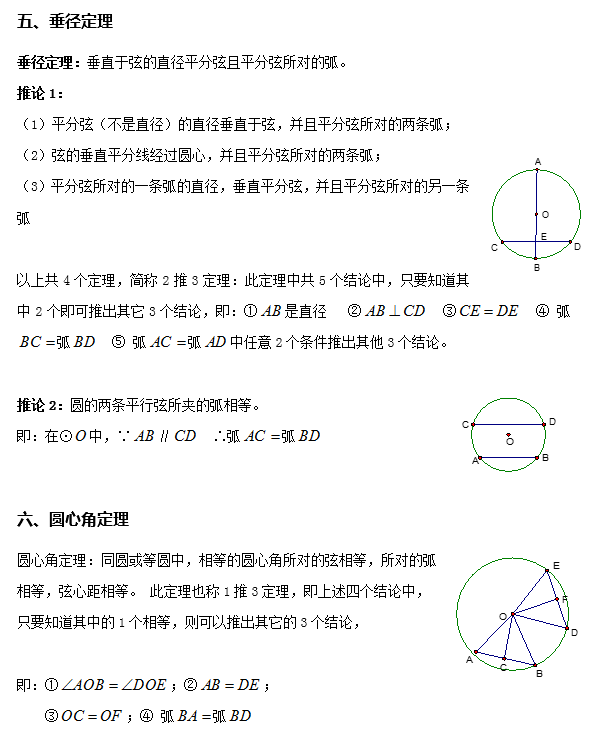
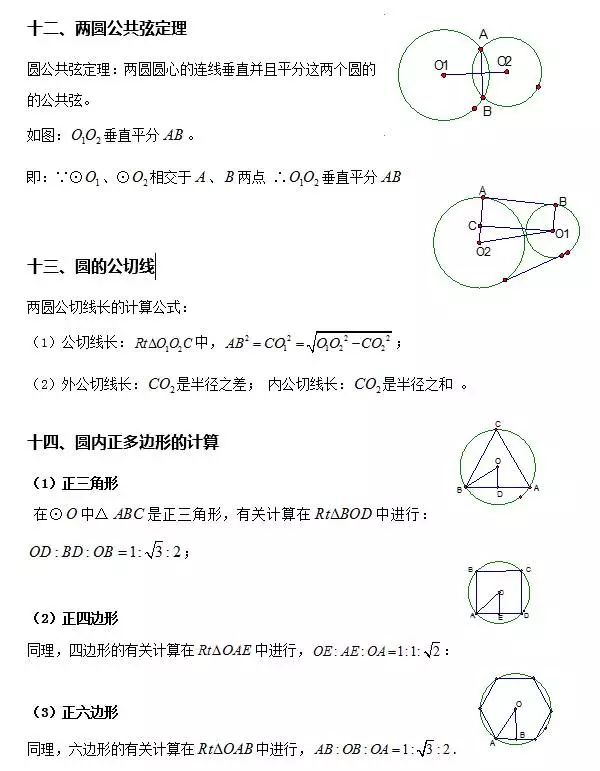
1. 遇到弦时（解决有关弦的问题时）

常常添加弦心距，或者作垂直于弦的半径（或直径）或再连结过弦的端点的半径。

作用：① 利用垂径定理；② 利用圆心角及其所对的弧、弦和弦心距之间的关系；③ 利用弦的一半、弦心距和半径组成直角三角形，根据勾股定理求有关量。

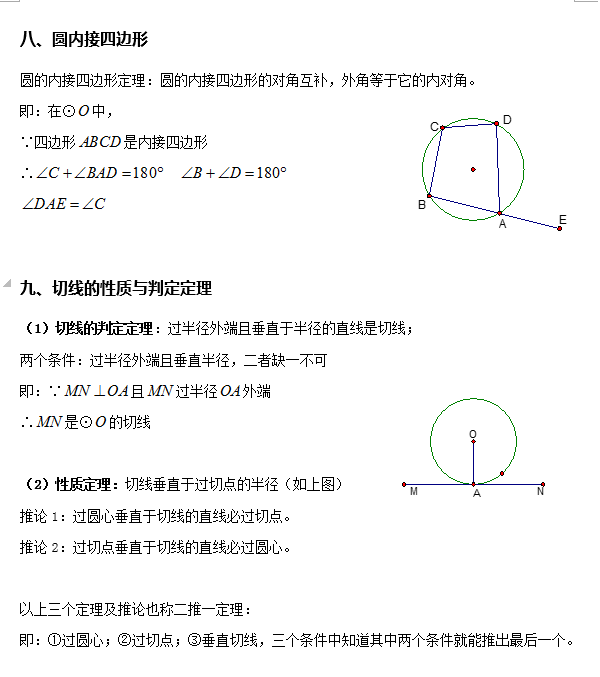
2. 遇到有直径时

常常添加（画）直径所对的圆周角

作用：利用圆周角的性质得到直角或直角三角形

3. 遇到90度的圆周角时

常常连结两条弦没有公共点的另一端点

作用：利用圆周角的性质，可得到直径

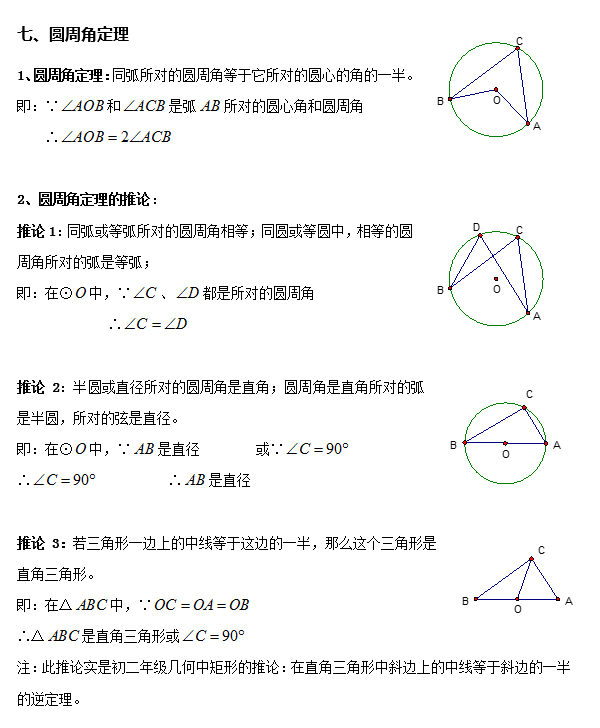
4. 遇到弦时

常常连结圆心和弦的两个端点，构成等腰三角形，还可连结圆周上一点和弦的两个端点。

作用：①可得等腰三角形；②据圆周角的性质可得相等的圆周角。

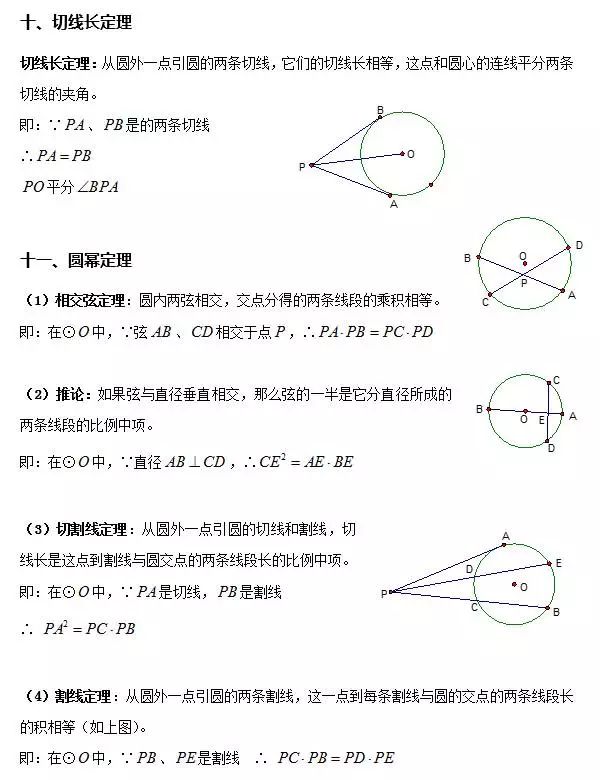
5. 遇到有切线时

常常添加过切点的半径（连结圆心和切点）；

作用：利用切线的性质定理可得OA⊥AB，得到直角或直角三角形。

常常添加连结圆上一点和切点；

作用：可构成弦切角，从而利用弦切角定理。

6. 遇到证明某一直线是圆的切线时

（1） 若直线和圆的公共点还未确定，则常过圆心作直线的垂线段。作用：若OA=r，则l为切线。

（2） 若直线过圆上的某一点，则连结这点和圆心（即作半径）作用：只需证OA⊥l，则l为切线。

（3） 有遇到圆上或圆外一点作圆的切线。

7. 遇到两相交切线时（切线长）

常常连结切点和圆心、连结圆心和圆外的一点、连结两切点。

作用：据切线长及其它性质，可得到

① 角、线段的等量关系  ② 垂直关系  ③ 全等、相似三角形

8. 遇到三角形的内切圆时

连结内心到各三角形顶点，或过内心作三角形各边的垂线段。作用：利用内心的性质，可得

① 内心到三角形三个顶点的连线是三角形的角平分线；

② 内心到三角形三条边的距离相等。

9. 遇到三角形的外接圆时

连结外心和各顶点

作用：外心到三角形各顶点的距离相等。

10. 遇到两圆外离时

（解决有关两圆的外、内公切线的问题）常常作出过切点的半径、连心线、平移公切线，或平移连心线。

作用：①利用切线的性质；②利用解直角三角形的有关知识。

11. 遇到两圆相交时

常常作公共弦、两圆连心线、连结交点和圆心等。

作用：①利用连心线的性质、解直角三角形有关知识；

② 利用圆内接四边形的性质；

③ 利用两圆公共的圆周的性质；④ 垂径定理。

12. 遇到两圆相切时

常常作连心线、公切线。

作用：①利用连心线性质；②切线性质等。

13. 遇到三个圆两两外切时

常常作每两个圆的连心线；作用：可利用连心线性质。

14. 遇到四边形对角互补时

常常添加辅助圆。作用：以便利用圆的性质。